| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 코딩 공부
- KITRI
- Blind SQL Injection
- bob 9기 후기
- 추리 소설
- webhacking.kr
- 백준
- 웹 개발
- 백준알고리즘
- 코딩
- 백엔드
- 가가 형사 시리즈
- 일본 소설
- 알고리즘
- 코딩공부
- 독서
- 히가시노 게이고
- 삼성 SW 역량 테스트
- Django Restful API
- DP
- serializer
- Django Rest Framework
- 정보 보안
- bob
- best of the best
- 백엔드 개발
- 동적 프로그래밍
- 백준 알고리즘
- Django CRUD
- 웹 해킹
- Today
- Total
요모조모 ʚɞ
[C] 백준 1106번 : 호텔 본문
오늘은 백준 1106번, 호텔을 풀어보았습니다 ꒰⑅ᵕ༚ᵕ꒱
원래는 7579번 앱을 풀려고 했는데,
시간 초과로 처참하게 실패한 후...
좀 더 쉬운 문제를 풀어보았답니다,,,
.
이번에도 저는 3단계에 걸쳐 문제를 풀었습니다!
1. 어떤 방식으로 해결할지 고민하기
2. 임의의 숫자를 대입하여 직접 풀어보기
3. 일반화해서 코드로 작성하기

https://www.acmicpc.net/problem/1106
1106번: 호텔
첫째 줄에 C와 형택이가 홍보할 수 있는 도시의 개수 N이 주어진다. C는 1,000보다 작거나 같은 자연수이고, N은 20보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 각 도시에서 홍보할 때 대는 비용과 그 비용으로 얻을 수 있는 고객의 수가 주어진다. 이 값은 100보다 작거나 같은 자연수이다.
www.acmicpc.net
1. 어떤 방식으로 해결할지 고민하기
저는 이 문제가 0/1 Knapsack인 것 같아
Dynamic Programming을 활용하였습니다.
(특정 도시를 홍보한다 or 안 한다 두 가지 선택지만 존재)
여기서 0/1 Knapsack 이란 흔히 배낭문제라고 불리는 알고리즘입니다.
.
쉽게 예시를 들어보자면 도둑이 물건을 훔친다고 했을 때,
A~D까지의 물건이 있고 각 물건은 가치가 다르며, 배낭의 크기 또한 정해져 있다고 합시다.
그렇다면 최대(혹은 최소)의 가치를 가지도록 물건을 훔치려면
어떤 물건들을 담아야할까요?
물건을 담는다, 안 담는다 이 두 가지 상태만 존재한다면 -> 0/1 Knapsack
물건을 쪼개어서라도 담을 수 있다면 -> fractional Knapsack
이라고 합니다.
.
보통
0/1 Knapsack -> Dynamic Programming 으로
fractional Knapsack -> Greedy 로 해결합니다.
.
따라서 저는 이 문제를 Dynamic Programming으로 해결하였고,
또 주어진 도시의 개수(=N)가 20 이하로 주어졌기 때문에 재귀 호출을 사용하였습니다.
-------------------------------------------------------------------------------------------------------------------
2. 임의의 숫자를 대입하여 직접 풀어보기

저는 문제에서 주어진 예시를 활용해보았습니다.
이해하기 쉽게 그래프를 그려보았는데
Node에는 남은 고객의 수 (누적 비용),
Edge는 선택한 index로 표현하였습니다.

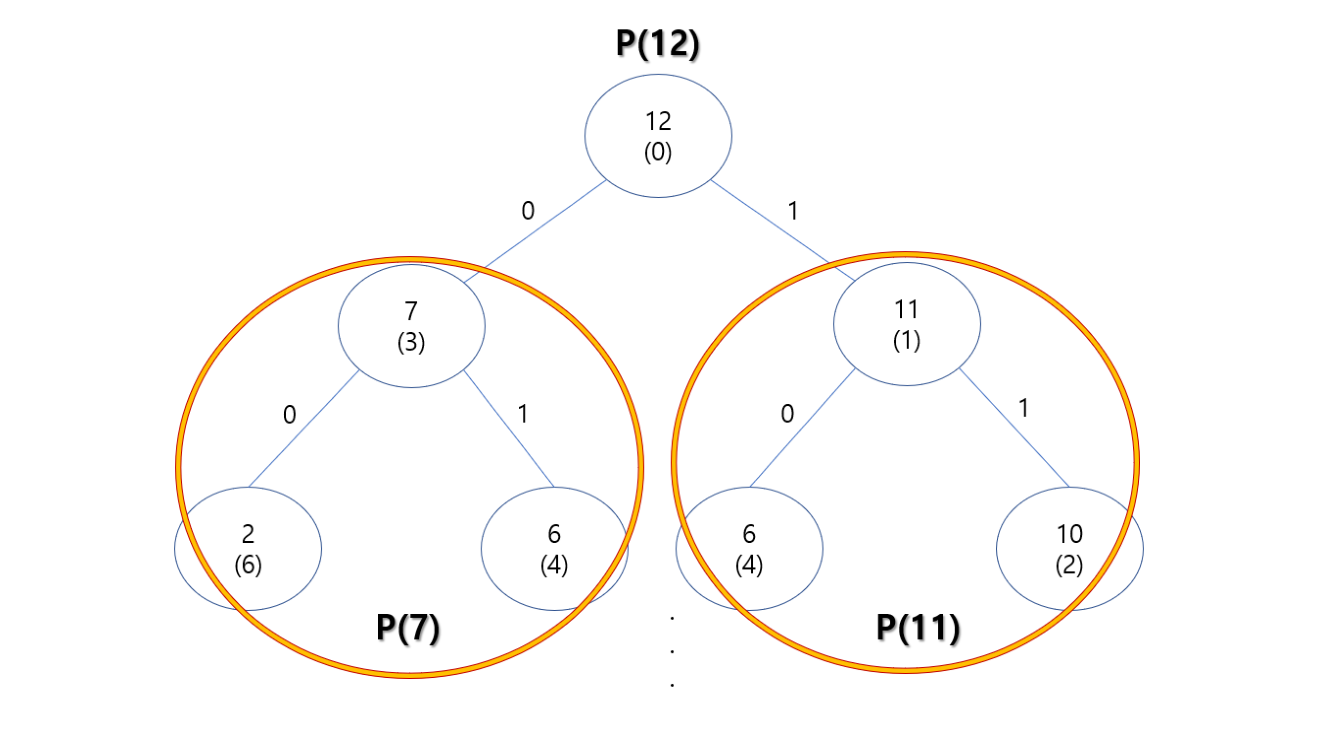


(여기서 P(N)은 고객이 N명 남았을 때의 해, 즉 N명을 홍보할 수 있는 최저 비용입니다.)
이렇게 표현을 하고 보니 이전에 구했던 작은 해를 통해 큰 해를 구할 수 있다는 걸 알게 되었습니다!
이제 이것을 코드로 표현해봅시다.
-------------------------------------------------------------------------------------------------------------------
3. 일반화해서 코드로 작성하기
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int info[20][2];
int sum[1001];
int advertisement(int customer, int cityNum)
{
int min = 100 * 1000;
int cost;
if (customer <= 0)
return 0;
else if (sum[customer] > 0)
return sum[customer];
else
{
for (int i = 0; i < cityNum; i++)
{
cost = advertisement(customer - info[i][1], cityNum) + info[i][0];
min = cost < min ? cost : min;
}
sum[customer] = min;
return min;
}
}
int main()
{
int c, n;
scanf("%d%d", &c, &n);
for (int i = 0; i < n; i++)
scanf("%d%d", &info[i][0], &info[i][1]);
printf("%d", advertisement(c, n));
}
제가 작성한 코드입니다!
info 배열의 0번째는 각 도시를 홍보하는데 드는 비용, 1번째에는 홍보 가능한 인원을 저장하였습니다.
그리고 저는 min 값을 100*1000 으로 설정하였습니다.
그 이유는 문제에서 주어진 홍보 비용은 최대 100원이라 하였고, 고객은 최대 1000명이라고 하였기 때문입니다.
저는 처음에 min 값을 대충 1000? 정도로 잡았다가 계속 오류가 났답니다... ʘ̥﹏ʘ
또한 sum이라는 배열을 별도로 선언하여 이전에 구해놓은 작은 해를 저장해두었습니다.
(이 배열을 따로 만들어주지 않았을 때는 시간 초과가 나왔던 걸로 기억합니다..!)
.
마지막으로 customer 값을 보았을 때
0보다 작거나 같으면 -> 이미 주어진 고객 수를 채웠기에 그래프를 더 깊숙하게 탐색할 필요 x (재귀 호출 종료)
sum[customer] >0이면 -> P(customer)를 구한 적이 있으니 다시 탐색할 필요 x
모두 아니면 -> P(customer)의 값을 구하자!
.
저는 이렇게 문제를 해결했습니다!
궁금한 점이나 이해가 안 가는 부분이 있으면 댓글 남겨주세요 •ܫ•
다음엔 재귀 호출이 아닌 다른 방법으로 Knapsack을 풀어보도록 하겠습니다..!
.
+) 4/30(목). 재귀호출이 아닌 다른 방법으로 문제를 다시 풀어보았습니다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#define MAX 100*1000
int cost[21], customer[21];
int dp[MAX + 1];
int max(int x, int y) {
return x > y ? x : y;
}
int main() {
int c, n;
// 입력
scanf("%d%d", &c, &n);
for (int i = 1; i <= n; i++)
scanf("%d%d", &cost[i], &customer[i]);
// dp 배열 구하기
for (int i = 1; i <= n; i++)
for (int j = cost[i]; j <= MAX; j++)
dp[j] = max(dp[j], dp[j - cost[i]] + customer[i]);
// 출력
for (int i = 1; i <= MAX; i++)
if (dp[i] >= c) {
printf("%d", i);
break;
}
return 0;
}'dp[비용] = 최대 고객'
으로 생각해서 문제를 풀었습니다 !
이렇게하면 c를 처음 넘는 비용이 정답입니다.
.
저는 재귀호출이 아닌 for문을 사용하면 실행시간을 줄일 수 있을거라 생각했습니다.
하지만 이 문제는 MAX 범위가 크고, n은 오히려 작게 주어졌기 때문에
재귀호출을 사용하는 것이 실행시간 측면에서 더 효율적이었습니다. (4ms 정도?)
큰 차이는 아니지만,
dp 배열보다 재귀호출을 구현하는 것이 더 쉽기 때문에
문제의 주어진 조건을 보고 적합한 방법을 선택하는 것이 좋을 것 같습니다 :-)
'코딩 > C' 카테고리의 다른 글
| [C] 백준 7579번 : 앱 (0) | 2020.04.28 |
|---|---|
| [C] 백준 2994번 : 내한 공연 (1) | 2020.04.27 |
| [C] 백준 1010번 : 다리 놓기 (0) | 2020.04.25 |
| [C] 백준 2960번 : 에라토스테네스의 체 (0) | 2020.04.18 |
| [C] 백준 11729번 : 하노이 탑 이동 순서 (0) | 2020.04.12 |




