| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- best of the best
- 코딩공부
- Django Restful API
- 웹 개발
- 알고리즘
- webhacking.kr
- 코딩
- 추리 소설
- 정보 보안
- serializer
- 삼성 SW 역량 테스트
- 동적 프로그래밍
- DP
- 백준알고리즘
- KITRI
- 코딩 공부
- 히가시노 게이고
- bob 9기 후기
- 백준 알고리즘
- Blind SQL Injection
- 가가 형사 시리즈
- 백준
- 백엔드 개발
- 백엔드
- bob
- Django CRUD
- 일본 소설
- Django Rest Framework
- 웹 해킹
- 독서
- Today
- Total
요모조모 ʚɞ
[C] 백준 7579번 : 앱 본문
오늘은 그동안 묵혀두었던 문제를 풀어보았습니다.. ´_ゝ`
그동안은 DP 문제를 풀 때 재귀 호출을 사용하거나 while 문을 이용해서 무작정 풀었었는데,
이번에는 그 방식들로는 문제가 풀리지 않았습니다. 시간 초과,,^^
그래서 DP를 다시 공부하고, 또 몇몇 해설을 참고한 후에 문제를 풀어보았습니다ㅜ
.
이 문제가 너무 어려우신 분들은 재귀 호출로 쉽게 풀 수 있는 1106번 먼저 풀어보시는 것을 추천드립니다! (더보기 참고)
https://www.acmicpc.net/problem/7579
7579번: 앱
입력은 3줄로 이루어져 있다. 첫 줄에는 정수 N과 M이 공백문자로 구분되어 주어지며, 둘째 줄과 셋째 줄에는 각각 N개의 정수가 공백문자로 구분되어 주어진다. 둘째 줄의 N개의 정수는 현재 활성화 되어 있는 앱 A1, ..., AN이 사용 중인 메모리의 바이트 수인 m1, ..., mN을 의미하며, 셋째 줄의 정수는 각 앱을 비활성화 했을 경우의 비용 c1, ..., cN을 의미한다 단, 1 ≤ N ≤ 100, 1 ≤ M ≤ 10,000,000이며, 1
www.acmicpc.net
우선 이 문제를 읽어보면, 0/1 knapsack 문제라는 것을 알 수 있습니다.
확보해야 하는 메모리 M -> 배낭의 크기
각 앱의 메모리 사용량 -> 물건의 크기
앱을 재 실행할 때 드는 비용 -> 물건의 비용
이라고 생각하면 쉽습니다!
따라서 저희는 동적 프로그래밍을 활용하여 코드를 작성해야 합니다.
+) N의 크기가 최대 100인 것을 보면 재귀 함수는 사용할 수 없음을 알 수 있습니다.
.
이번 문제는 이해하기 쉽도록 코드를 보면서 설명하겠습니다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#define MAX(x, y) x>y?x:y
int memory[101], cost[101];
int dp[100 * 100 + 1];
int main() {
int N, M;
// 입력
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; i++)
scanf("%d", &memory[i]);
for (int i = 1; i <= N; i++)
scanf("%d", &cost[i]);
// dp 배열 채우기
for (int i = 1; i <= N; i++)
for (int j = 100 * 100; j >= 0; j--) {
if (j < cost[i])
break;
dp[j] = MAX(dp[j], dp[j - cost[i]] + memory[i]);
}
// 출력
for (int i = 0; i <= 100 * 100; i++)
if (dp[i] >= M){
printf("%d", i);
break;
}
return 0;
}
저는 구한 값들을 저장하기 위해 dp라는 배열을 따로 선언하였습니다.
그리고 여기서 dp의 index는 비활성화 비용, 값은 메모리로 사용하였습니다.
즉, dp 배열은 해당 비활성화 비용으로 확보할 수 있는 메모리의 양을 의미합니다.
(비활성화 비용을 다 쓰는 것 x, 최대로 쓸 수 있는 비용)
여기서 주의할 점은 같은 비용으로 구할 수 있는 메모리가 여러 case로 존재한다는 점입니다.
저는 이 case들 중 최대 메모리 값을 dp에 저장하였습니다.
왜냐하면 비용이 같을 때 최대 메모리 양을 가지는 것이 최소 비용을 찾는 데 더욱 유리하기 때문입니다.
이렇게 구한 dp 배열은 i를 반복함에 따라 계속 update 되면서 최적화 값에 가까워집니다!
=> dp [비용] = 구할 수 있는 최대 메모리
.
이해하기 쉽도록 간단한 예시를 들어보겠습니다.

dp 배열의 모습을 간단한 그림으로 표현하면 다음과 같습니다.
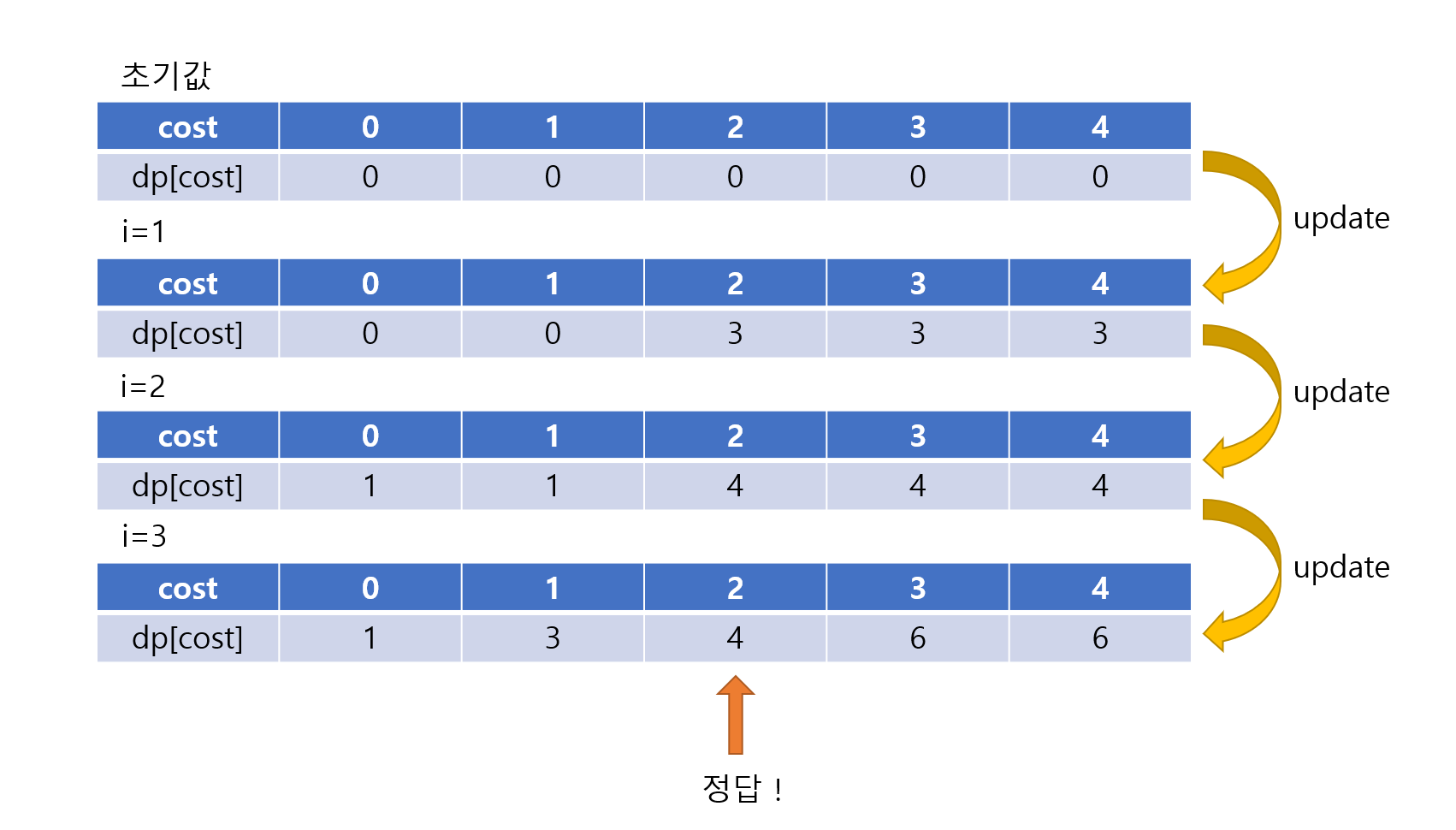
dp 배열은 i와 j가 반복됨에 따라 점점 최적화된 값을 가진다는 것을 볼 수 있습니다.
또한 이 표를 활용하면 정답은 dp [2]=4 임을 쉽게 구할 수 있습니다!
(dp [2]=4가 의미하는 바는 '2라는 비용을 사용하여 최대 4의 메모리를 비활성화할 수 있다'입니다.)
다른 것이 답이 아닌 이유는 dp [1]의 경우 구할 수 있는 최대 메모리가 3밖에 안되고,
dp [3]의 경우에는 구할 수 있는 메모리가 6이지만 최소의 비용이 아니기 때문입니다. (dp [2]가 이미 있음)
=> dp 배열의 update가 끝난 후 문제에서 주어진 메모리 조건을 처음으로 만족하는 것이 정답! (최저 index)
.
저는 편의상 j의 범위를 4까지만 표현하였는데, 코드 상에서는 j를 cost의 최대 범위로 잡아주어야 합니다.
cost의 총합이 얼마까지 증가할지는 알 수 없기 때문입니다.
따라서 저는 문제 조건인 N <=100과 C <=100을 참고하여 100*100으로 잡아주었습니다.
.
코드 자체는 굉장히 간단하지만 ㅠㅠ 생각해내는 것이 어려웠던 문제입니다.
하지만 확실히 실행시간이 재귀 호출이나 while문으로 풀 때보다 줄어들었습니다.
이 문제의 경우 N*100*100 으로 해결할 수 있습니다. O(N)이라고 하면 되는 건가..?
.
혹시 틀린 부분이나 이해 안 가는 부분이 있다면 댓글 남겨주세요 :)
'코딩 > C' 카테고리의 다른 글
| [C] 백준 2294번 : 동전 2 (0) | 2020.04.30 |
|---|---|
| [C] 백준 1915번 : 가장 큰 정사각형 (0) | 2020.04.29 |
| [C] 백준 2994번 : 내한 공연 (1) | 2020.04.27 |
| [C] 백준 1010번 : 다리 놓기 (0) | 2020.04.25 |
| [C] 백준 2960번 : 에라토스테네스의 체 (0) | 2020.04.18 |




