[C] 백준 1915번 : 가장 큰 정사각형
오늘은 새로운 DP 문제를 풀어보았습니다 ✿
이 문제는 '7579번 앱'의 순한 맛 같은 느낌이라ㅎ,,
어제보다는 빨리 푼 것 같아요 !
.
이번 문제 역시 총 3단계에 걸쳐 풀어보았습니다.
1. 어떤 방식으로 해결할지 고민하기
2. 임의의 숫자를 대입하여 직접 풀어보기
3. 일반화해서 코드로 작성하기

https://www.acmicpc.net/problem/1915
1915번: 가장 큰 정사각형
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
www.acmicpc.net
1. 어떤 방식으로 해결할지 고민하기
우선 이 문제에서 정사각형을 탐색하려면 각 행과 그 행에 대한 열을 하나씩 탐색해야 합니다.
그렇게 탐색을 해나가다 보면, 구한 정사각형의 최댓값이 변화하게 됩니다. (점점 최적화되어감)
따라서 저는 정사각형에 대한 정보를 dp라는 배열에 저장해놓고,
이를 점점 최적화해나가다 보면 정답을 구할 수 있을 것이라 생각하였습니다.
=> 동적 프로그래밍으로 풀기
-------------------------------------------------------------------------------------------------------------------
2. 임의의 숫자를 대입하여 직접 풀어보기
저는 문제에서 주어진 예시를 대입하여 직접 풀어보았습니다.

그냥 무작정 풀기보다는, 나름의 규칙성을 찾아보려고 노력하였습니다.
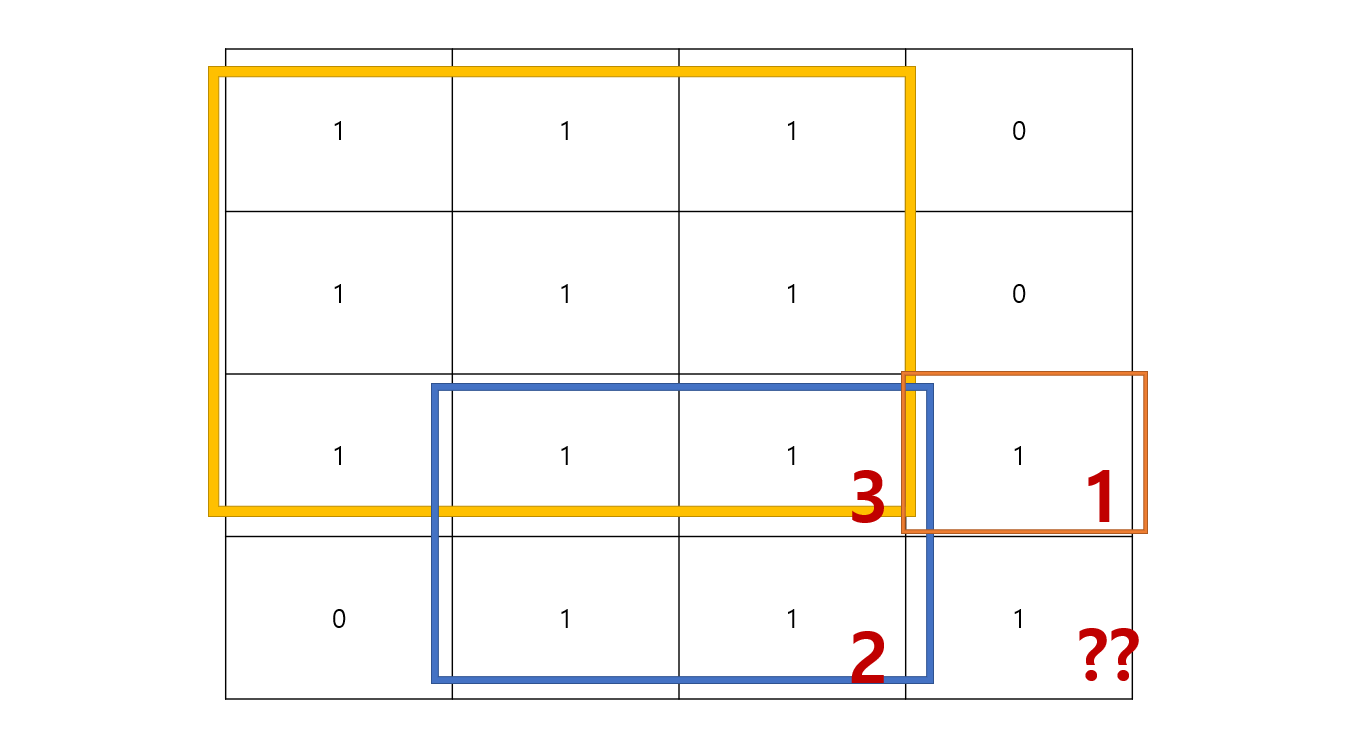
따라서 아래의 그림과 같이 dp[i][j]일 때의 탐색 범위를 ①, ②, ③으로 나누어 생각해보았습니다.
(참고로 dp[i][j]에 들어있는 값은 입력받은 배열 i행 j열의 값으로 만들 수 있는 최대 정사각형 한 변의 길이)

제가 몇 가지 규칙들을 찾아보았는데 그것은 다음과 같습니다.
1) ①, ②, ③ 中 하나라도 0 이면 -> dp[i][j] = 1
2) ① = ② = ③ 이면 -> dp[i][j] = dp[i][j-1] + 1 (① + 1)
3) ① = ② or ② = ③ 이면 -> dp[i][j] = dp[i-1][j-1] + 1 (② + 1)
4) ① != ② != ③ 이면 -> ①, ②, ③ 中 제일 작은 애 + 1
이 규칙은 주어진 예시를 직접 풀어보면 쉽게 구할 수 있습니다.
.
4번 규칙은 다음과 같은 예시를 풀어보면 구할 수 있습니다!

-------------------------------------------------------------------------------------------------------------------
3. 일반화해서 코드로 작성하기
저는 처음 문제를 풀 때는 제가 대충 모든 규칙을 찾았다고 생각해서,
저 4가지 케이스로만 문제를 풀었습니다.
하지만 ,, 역시는 역시 ... 틀렸다고 나오더라구요 .. ^^
.
그래서 다른 케이스가 더 있나? 아니면 내가 틀린 규칙을 찾았나? 고민하던 차에
4번 규칙을 보고 새로운 생각이 하나 떠올랐습니다!

위의 그림과 같이 ①의 값이 a, ②의 값이 b, ③의 값이 c라고 생각을 해봅시다.
참고로 dp[i][j]는 '입력받은 배열 i행 j열의 값으로 만들 수 있는 최대 정사각형 한 변의 길이'입니다.
따라서 입력받은 배열의 값이 0일 때는 고려하지 않고, 1일 때만 dp배열을 채워주면 됩니다.
그렇다면 위 그림의 경우도 입력받은 배열의 i행 j열이 1일 때를 나타내는 것이겠죠 ?!
.
dp 배열의 의미를 잘 이해했다면 위의 상황은
①을 통해 한 변의 길이가 a인 정사각형을 만듦
②을 통해 한 변의 길이가 b인 정사각형을 만듦
③을 통해 한 변의 길이가 c인 정사각형을 만듦
임을 알 수 있습니다.
따라서 입력받은 배열 i행 j열 또한 값이 1이라면 ①, ②, ③의 값을 활용하여 dp[i][j]를 구할 수 있습니다.
dp[i][j]는 a와 b, c 중 제일 작은 값에 1을 더해주면 됩니다.
=> dp[i][j] = min(a, b, c)+1
.
이해를 잘 안 간다면 밑의 예시를 참고해주세요!
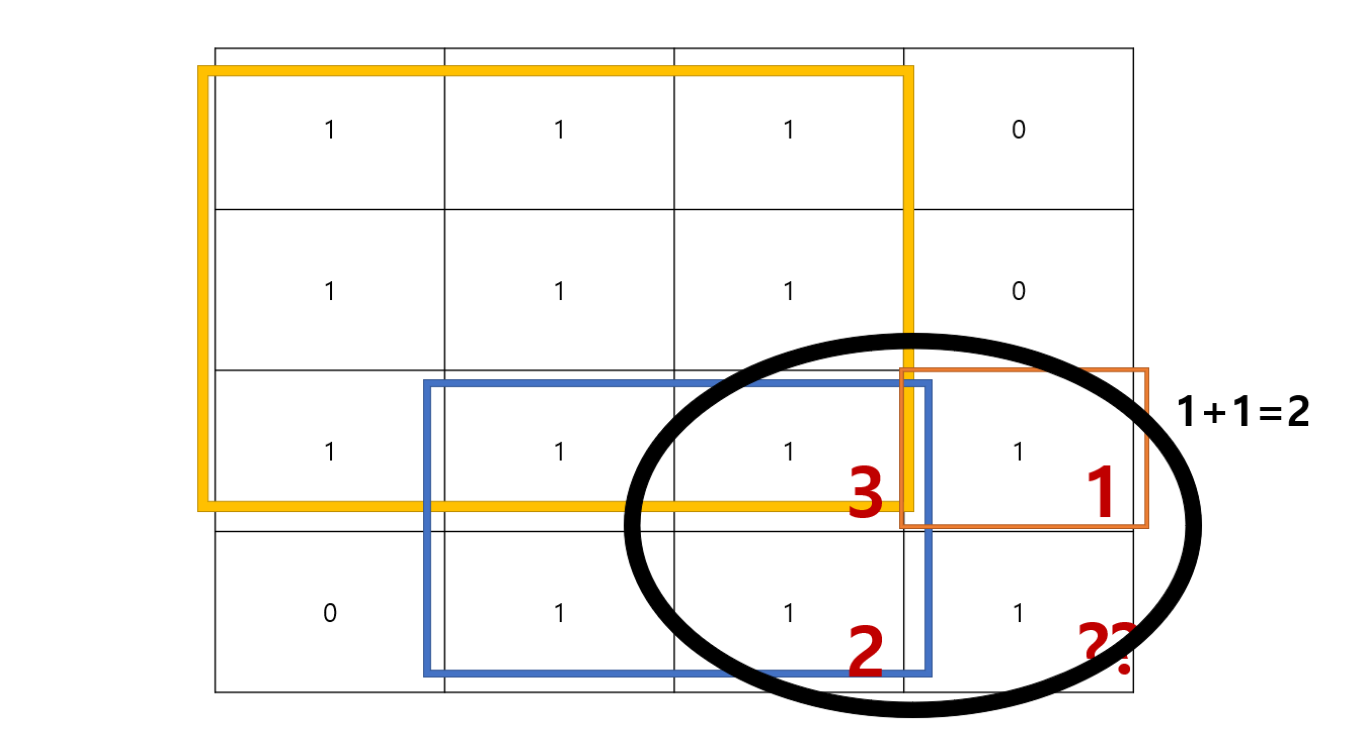
위의 예시처럼 ①, ②, ③ 중 제일 작은 것을 위주로 새로운 정사각형의 경계를 잡아야 합니다.
그리고 지금 찾고자 하는 값 또한 정사각형에 포함해야 하기 때문에 1을 더해주는 것입니다.
즉, 이 예시에서는 1+1=2라고 생각하시면 됩니다.
.
다음은 제가 구현한 코드입니다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int input[1001][1001];
int dp[1001][1001];
int min(int x, int y) {
return x < y ? x : y;
}
int main() {
int n, m;
char line[1000];
int max = 0;
// 입력
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%s", line);
for (int j = 0; j < m; j++)
input[i][j + 1] = line[j]-'0';
}
// dp 배열 채우기
int value1, value2;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (input[i][j] == 0)
continue;
dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j - 1]), dp[i-1][j])+1;
if (max < dp[i][j])
max = dp[i][j];
}
// 출력
printf("%d", max*max);
return 0;
}
dp 배열을 구하는 것은 앞서 설명했던 것과 같이 input[i][j]가 1일 때만 고려하면 되고,
①, ②, ③의 값 중 제일 작은 값에 1을 더하면 됩니다.
그리고 최종적으로 구해야 할 최대 정사각형 변의 길이를 계속 update 해줍니다!
.
또 입력 시 주의해야 할 것이 있는데, 기존의 문제들과는 다르게 정수 입력이 띄어쓰기 없이 들어왔습니다.
(ex. 1 0 1 0 이라면 1010이라고 입력이 들어온 격)
따라서 저는 입력을 문자열로 받고, 이것을 하나씩 정수로 변환해주었습니다.
(문자를 '0'로 빼주면 정수가 됩니다.)
.
이번 문제 역시 코드 자체가 간단하였지만, 일반화하는 것이 어려웠습니다ㅠ
코드를 작성하는 것보다는, 완전한 일반화 식을 구하는 것에 좀 더 노력을 기울어야 할 것 같습니다 ㅜ.ㅜ