[C] 백준 1010번 : 다리 놓기

 

오늘은 오랜만에 ,, 새로운 문제를 풀어보았습니다 ! .. ✎

백준 1010번 다리 놓기 문제입니다.

 

백준 1010번

https://www.acmicpc.net/problem/1010

1010번: 다리 놓기

 

1010번 문제의 포인트는 다리끼리는 서로 겹칠 수 없다는 점입니다 ! ✦

이 점에 좀 더 유의하여 고민해보니, 이번 문제가 고등학교 때 배웠던 조합?과 연관이 있음을 느꼈습니다.

조합이란 서로 다른 n개 중에서 r개(n≥r)를 택하는 경우를 의미하고, 이를 nCr이라고 표현합니다.

이 개념을 1010번 문제에 적용해보면, M개의 사이트 중에 N개를 골라 위에서 부터 1:1로 연결한다고 생각하면 됩니다.

.

이 문제를 조합으로 풀 수 있다면 코드 자체가 굉장히 간단할 것이라 생각했는데,, 생각보다 시행착오를 많이 겪었습니다...^^ㅠ

계산된 조합이 int 범위를 벗어나는 경우가 생겨서 자료형을 int가 아닌 다른 것으로 수정해주어야 했습니다. (ex. double, long long)

우선 제가 시도한 3가지 방법을 소개하겠습니다.

.

① 첫번째로 생각해낸 방법은 아마 대부분의 사람들이 가장 먼저 떠올리는 방법일 것입니다.

바로 조합의 공식을 이용하는 것입니다. 

조합 공식

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

double factorial(int n) {
	if (n == 0)
		return 1;
	return n * factorial(n - 1);
}

double combination(int n, int m) {
	return factorial(n) / (factorial(n - m)*factorial(m));
}

int main()
{
	int T, N, M;

	scanf("%d", &T);
	for (int i = 0; i < T; i++) {
		scanf("%d%d", &N, &M);
		printf("%.lf\n",combination(M, N));
	}

	return 0;
}

저는 이 공식을 계산하기 위해 factorial 함수를 따로 만들어주었습니다.

그리고 원래는 long long 자료형을 사용하려고 했는데, factorial을 계산하다 보면 long long의 범위를 초과할 때가 발생해서 모두 다 double을 사용해주었습니다. 만능 double..

.

② 처음에 1번 방법을 시도해보았을 때 답이 틀렸다고 나오기에, 시간이 초과되는 건줄 알고 다른 방법을 구상하였습니다. (알고 보니 그냥 자료형이 틀린 문제였던..)

바로 조합의 성질 중 하나를 사용하는 방법입니다.

조합의 성질

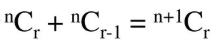
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

double combination(int n, int m) {
	if (n == m)
		return 1;
	if (m == 1)
		return n;
	return combination(n - 1, m - 1) + combination(n - 1, m);
}

int main()
{
	int T, N, M;

	scanf("%d", &T);
	for (int i = 0; i < T; i++) {
		scanf("%d%d", &N, &M);
		printf("%.lf\n", combination(M, N));
	}

	return 0;
}

두 번째 방법은 역시 재귀호출을 사용하지만, factorial 함수 없이 풀 수 있었습니다.

다만,, 이 방법은 첫번째 방법보다 실행시간이 더 많이 걸렸답니다...ㅎ (완전 턱걸이로 정답)

.

③ 마지막으로는 2번과 동일한 성질을 사용하되, 재귀 함수 없이 문제를 풀어보았습니다 !

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

long long c[30][30];

void combination() // n >= m
{
	for (int i = 1; i < 30; i++) {
		c[i][i] = 1;
		c[i][1] = i;
	}
	for (int i = 2; i < 30; i++) {
		for (int j = 2; j < 30; j++) {
			if (i>j)
				c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
		}
	}
}

int main()
{
	int T, N, M;
	scanf("%d", &T);

	combination();

	for (int i = 0; i < T; i++) {
		scanf("%d%d", &N, &M);
		printf("%lld\n", c[M][N]);
	}

	return 0;
}

c라고 하는 별도의 2차원 배열을 사용하여, 주어진 index에 해당하는 조합의 값을 저장하였습니다.

(ex. nCr -> c[n][r]에 저장)

또한 combination 함수에서 m이 n보다 클 수는 없기 때문에 (nCr을 생각해보면 n≥r) if 문을 사용하여 대입 횟수를 줄여주었습니다.

.

이 문제는 알고리즘 자체만 놓고 보면 굉장히 간단하지만, 자료형을 조심하지 않으면 한참을 헤매게 됩니다,, ꃼ.̫ ꃼ 

제가 int 이외의 다른 정수형 자료형을 사용해본 적이 거의 없어서 앞으로 자료형에 대해 좀 더 공부해보아야겠다고 느꼈습니다...ㅠ